This tutorial covers the creation of a ragdoll physics simulation using PyODE, the Python bindings for the Open Dynamics Engine. This tutorial assumes a basic understanding of Python and ODE, and knowledge of basic OpenGL programming is helpful but not strictly necessary.
While this tutorial is intended to be both useful and informative, and all code necessary to implement it in stages may be copied and pasted directly from this page into a single Python source file, the impatient who simply want to get a ragdoll simulation up and running right away you can download the complete source code directly. All source code provided for this tutorial is covered by the BSD license.
Although written in Python the techniques used should be easily transferable to ODE simulations written in C or C++. If any reader would like to translate this tutorial to C/C++ I'd be happy to host it as a separate download.
NOTE: this tutorial received a recent bugfix to correct missing collisions when run with some versions of Python due to the capsule geoms being garbage collected immediately after creation.
Here's a video of the ragdoll in action:
Prep Work
Before jumping right in and building a ragdoll we need to import the necessary modules, define useful utility functions, and provide the necessary initialization and callback functions for the ODE simulation and OpenGL display. Much of the initialization and callback code here has been modified from code in the official PyODE tutorials.
We'll start by importing modules and defining basic vector operations, as well as matrix operations for defining rotations in 3D. Many of these functions are handy to keep around for miscellaneous 3D graphics or simulation coding in Python:
import sys, os, random, time from math import * from OpenGL.GL import * from OpenGL.GLU import * from OpenGL.GLUT import * import ode def sign(x): """Returns 1.0 if x is positive, -1.0 if x is negative or zero.""" if x > 0.0: return 1.0 else: return -1.0 def len3(v): """Returns the length of 3-vector v.""" return sqrt(v[0]**2 + v[1]**2 + v[2]**2) def neg3(v): """Returns the negation of 3-vector v.""" return (-v[0], -v[1], -v[2]) def add3(a, b): """Returns the sum of 3-vectors a and b.""" return (a[0] + b[0], a[1] + b[1], a[2] + b[2]) def sub3(a, b): """Returns the difference between 3-vectors a and b.""" return (a[0] - b[0], a[1] - b[1], a[2] - b[2]) def mul3(v, s): """Returns 3-vector v multiplied by scalar s.""" return (v[0] * s, v[1] * s, v[2] * s) def div3(v, s): """Returns 3-vector v divided by scalar s.""" return (v[0] / s, v[1] / s, v[2] / s) def dist3(a, b): """Returns the distance between point 3-vectors a and b.""" return len3(sub3(a, b)) def norm3(v): """Returns the unit length 3-vector parallel to 3-vector v.""" l = len3(v) if (l > 0.0): return (v[0] / l, v[1] / l, v[2] / l) else: return (0.0, 0.0, 0.0) def dot3(a, b): """Returns the dot product of 3-vectors a and b.""" return (a[0] * b[0] + a[1] * b[1] + a[2] * b[2]) def cross(a, b): """Returns the cross product of 3-vectors a and b.""" return (a[1] * b[2] - a[2] * b[1], a[2] * b[0] - a[0] * b[2], a[0] * b[1] - a[1] * b[0]) def project3(v, d): """Returns projection of 3-vector v onto unit 3-vector d.""" return mul3(v, dot3(norm3(v), d)) def acosdot3(a, b): """Returns the angle between unit 3-vectors a and b.""" x = dot3(a, b) if x < -1.0: return pi elif x > 1.0: return 0.0 else: return acos(x) def rotate3(m, v): """Returns the rotation of 3-vector v by 3x3 (row major) matrix m.""" return (v[0] * m[0] + v[1] * m[1] + v[2] * m[2], v[0] * m[3] + v[1] * m[4] + v[2] * m[5], v[0] * m[6] + v[1] * m[7] + v[2] * m[8]) def invert3x3(m): """Returns the inversion (transpose) of 3x3 rotation matrix m.""" return (m[0], m[3], m[6], m[1], m[4], m[7], m[2], m[5], m[8]) def zaxis(m): """Returns the z-axis vector from 3x3 (row major) rotation matrix m.""" return (m[2], m[5], m[8]) def calcRotMatrix(axis, angle): """ Returns the row-major 3x3 rotation matrix defining a rotation around axis by angle. """ cosTheta = cos(angle) sinTheta = sin(angle) t = 1.0 - cosTheta return ( t * axis[0]**2 + cosTheta, t * axis[0] * axis[1] - sinTheta * axis[2], t * axis[0] * axis[2] + sinTheta * axis[1], t * axis[0] * axis[1] + sinTheta * axis[2], t * axis[1]**2 + cosTheta, t * axis[1] * axis[2] - sinTheta * axis[0], t * axis[0] * axis[2] - sinTheta * axis[1], t * axis[1] * axis[2] + sinTheta * axis[0], t * axis[2]**2 + cosTheta) def makeOpenGLMatrix(r, p): """ Returns an OpenGL compatible (column-major, 4x4 homogeneous) transformation matrix from ODE compatible (row-major, 3x3) rotation matrix r and position vector p. """ return ( r[0], r[3], r[6], 0.0, r[1], r[4], r[7], 0.0, r[2], r[5], r[8], 0.0, p[0], p[1], p[2], 1.0)
Next we add a function to create an ODE capsule. A benefit of using PyODE is that ODE bodies are Python objects instead of handles (integer references), and Python makes it easy to extend objects of any class. Here we store the radius and length of the capsule directly in the capsule ode.Body object.
def createCapsule(world, space, density, length, radius): """Creates a capsule body and corresponding geom.""" # create capsule body (aligned along the z-axis so that it matches the # GeomCCylinder created below, which is aligned along the z-axis by # default) body = ode.Body(world) M = ode.Mass() M.setCappedCylinder(density, 3, radius, length) body.setMass(M) # set parameters for drawing the body body.shape = "capsule" body.length = length body.radius = radius # create a capsule geom for collision detection geom = ode.GeomCCylinder(space, radius, length) geom.setBody(body) return body, geom
ODE also requires a callback function for handling collisions between ODE bodies. This function is quite basic, setting a universal friction coefficient for all collisions. Feel free to modify this value while experimenting with this tutorial. The default value of 500 is good for fairly typical collisions, 5000 is very sticky and can pin limbs in awkward positions, 50 is like sliding on ice, while 0 offers no friction. In a more realistic simulation with a complete environment you will want to replace this function with one which determines a friction coefficient from the interaction of the material types of both colliding surfaces. You can also play around with the bounce value, but to simulate a realistic human body this value should be fairly low. 0.2 seems to work well.
Also note that collisions between bodies sharing a joint are ignored. While it is possible to build a ragdoll where all body parts collide with each other, doing so would require large gaps around each joint and could restrict range of motion (imagine building an arm out of two capsules, and trying to bend the elbow without the two capsules touching). Here is the collision callback:
def near_callback(args, geom1, geom2): """ Callback function for the collide() method. This function checks if the given geoms do collide and creates contact joints if they do. """ if (ode.areConnected(geom1.getBody(), geom2.getBody())): return # check if the objects collide contacts = ode.collide(geom1, geom2) # create contact joints world, contactgroup = args for c in contacts: c.setBounce(0.2) c.setMu(500) # 0-5 = very slippery, 50-500 = normal, 5000 = very sticky j = ode.ContactJoint(world, contactgroup, c) j.attach(geom1.getBody(), geom2.getBody())
Below this add the necessary OpenGL graphics functions including initialization, capsule rendering (capsules are the ODE geometry type which will be used for all body parts), and the GLUT (GL Utility Toolkit) callback functions which will handle display, keyboard input, and the idle processing time where the ODE simulation occurs. This code will not be discussed in any more detail except to note the the simulation can be quit by pressing 'Q', and that pressing a number key will enter a slow motion mode: '9' for most slowdown, '1' for least slowdown, and '0' to return to normal speed.
Note that the draw and idle callbacks reference an object named ragdoll. We haven't defined this yet so after adding this code the program won't run, but we'll fix that soon by adding a very simple version of a ragdoll. At this point the code using ragdoll merely renders its component bodies and performs an update within each iteration of the simulation loop. This update will eventually perform the work of simulating the resistive forces in certain joints that cannot be capture using ODE joint types and stops alone.
def prepare_GL(): """Setup basic OpenGL rendering with smooth shading and a single light.""" glClearColor(0.8, 0.8, 0.9, 0.0) glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); glEnable(GL_DEPTH_TEST) glEnable(GL_LIGHTING) glEnable(GL_NORMALIZE) glShadeModel(GL_SMOOTH) glMatrixMode(GL_PROJECTION) glLoadIdentity() gluPerspective (45.0, 1.3333, 0.2, 20.0) glViewport(0, 0, 640, 480) glMatrixMode(GL_MODELVIEW) glLoadIdentity() glLightfv(GL_LIGHT0,GL_POSITION,[0, 0, 1, 0]) glLightfv(GL_LIGHT0,GL_DIFFUSE,[1, 1, 1, 1]) glLightfv(GL_LIGHT0,GL_SPECULAR,[1, 1, 1, 1]) glEnable(GL_LIGHT0) glEnable(GL_COLOR_MATERIAL) glColor3f(0.8, 0.8, 0.8) gluLookAt(1.5, 4.0, 3.0, 0.5, 1.0, 0.0, 0.0, 1.0, 0.0) # polygon resolution for capsule bodies CAPSULE_SLICES = 16 CAPSULE_STACKS = 12 def draw_body(body): """Draw an ODE body.""" rot = makeOpenGLMatrix(body.getRotation(), body.getPosition()) glPushMatrix() glMultMatrixd(rot) if body.shape == "capsule": cylHalfHeight = body.length / 2.0 glBegin(GL_QUAD_STRIP) for i in range(0, CAPSULE_SLICES + 1): angle = i / float(CAPSULE_SLICES) * 2.0 * pi ca = cos(angle) sa = sin(angle) glNormal3f(ca, sa, 0) glVertex3f(body.radius * ca, body.radius * sa, cylHalfHeight) glVertex3f(body.radius * ca, body.radius * sa, -cylHalfHeight) glEnd() glTranslated(0, 0, cylHalfHeight) glutSolidSphere(body.radius, CAPSULE_SLICES, CAPSULE_STACKS) glTranslated(0, 0, -2.0 * cylHalfHeight) glutSolidSphere(body.radius, CAPSULE_SLICES, CAPSULE_STACKS) glPopMatrix() def onKey(c, x, y): """GLUT keyboard callback.""" global SloMo, Paused # set simulation speed if c >= '0' and c <= '9': SloMo = 4 * int(c) + 1 # pause/unpause simulation elif c == 'p' or c == 'P': Paused = not Paused # quit elif c == 'q' or c == 'Q': sys.exit(0) def onDraw(): """GLUT render callback.""" prepare_GL() for b in bodies: draw_body(b) for b in ragdoll.bodies: draw_body(b) glutSwapBuffers() def onIdle(): """GLUT idle processing callback, performs ODE simulation step.""" global Paused, lasttime, numiter if Paused: return t = dt - (time.time() - lasttime) if (t > 0): time.sleep(t) glutPostRedisplay() for i in range(stepsPerFrame): # Detect collisions and create contact joints space.collide((world, contactgroup), near_callback) # Simulation step (with slo motion) world.step(dt / stepsPerFrame / SloMo) numiter += 1 # apply internal ragdoll forces ragdoll.update() # Remove all contact joints contactgroup.empty() lasttime = time.time()
Now add the final components of the program shell: creating the application window, setting up the ODE simulation, registering the GLUT callbacks, and entering the event loop. Once again we introduce a few unmet dependencies, this time on the RagDoll class, which will be introduced in the next section.
# initialize GLUT
glutInit([])
glutInitDisplayMode(GLUT_RGB | GLUT_DEPTH | GLUT_DOUBLE)
# create the program window
x = 0
y = 0
width = 640
height = 480
glutInitWindowPosition(x, y);
glutInitWindowSize(width, height);
glutCreateWindow("PyODE Ragdoll Simulation")
# create an ODE world object
world = ode.World()
world.setGravity((0.0, -9.81, 0.0))
world.setERP(0.1)
world.setCFM(1E-4)
# create an ODE space object
space = ode.Space()
# create a plane geom to simulate a floor
floor = ode.GeomPlane(space, (0, 1, 0), 0)
# create a list to store any ODE bodies which are not part of the ragdoll (this
# is needed to avoid Python garbage collecting these bodies)
bodies = []
# create a joint group for the contact joints generated during collisions
# between two bodies collide
contactgroup = ode.JointGroup()
# set the initial simulation loop parameters
fps = 60
dt = 1.0 / fps
stepsPerFrame = 2
SloMo = 1
Paused = False
lasttime = time.time()
numiter = 0
# create the ragdoll
ragdoll = RagDoll(world, space, 500, (0.0, 0.9, 0.0))
print "total mass is %.1f kg (%.1f lbs)" % (ragdoll.totalMass,
ragdoll.totalMass * 2.2)
# set GLUT callbacks
glutKeyboardFunc(onKey)
glutDisplayFunc(onDraw)
glutIdleFunc(onIdle)
# enter the GLUT event loop
glutMainLoop()
Creating The Body
Now that the shell of the simulation is in place it's time to create an initial version of the ragdoll body with joints. We'll start by defining the parts of the body and attaching them together with fixed joints or ball joints, the easiest types of joints to create in ODE because neither requires any defined rotation axes. Later we'll upgrade the ragdoll by replacing some ball joints with more realistic hinge and universal joints, and augmenting the shoulder ball joints with custom code prevent unrestricted movement.
In developing this simulation the most tedious aspect was not coding, but making accurate measurements of an actual human body (in my case, my own) get the ragdoll to look and behave correctly. Although it's possible to get started by just making educated guesses, in the end the ragdoll won't look or behave quite right (especially one as complex as we're about to create), and it will save time to make good measurements up front. Fortunately for you, I'm an extremely average proportioned adult male (5'10" tall, about 155 lbs) and so the dimensions provided in this tutorial should be a good starting point for your simulation. Different bodies you may wish to simulate will of course vary a bit in size and shape, but starting from a good prototype should make the process easier.
Before getting to my measurements it's important to make a note about the method I used to model the ragdoll. Each rigid body in the ragdoll is a capsule, and ODE makes it easy to make bodies sharing joints to penetrate without generating collisions. However, you generally don't want other pairs of bodies to be able penetrate, and here we can run into problems. I started out by making the capsule endpoints of each body directly overlap the shared joint, creating joints were fairly seamless (see first image below). This worked great at the wrists, ankles, elbows, and knees, but the upper arms and legs ended up occasionally bumping into the mid-torso capsule, restricting these joint's rotations. Shrinking the torso is a possible workaround, but the result is unrealistically skinny. At the other extreme is making the capsules barely touch (last image below). This will eliminate internal ragdoll collisions, but leave gaps at the joints that could make collisions with external objects unrealistic. In the end I compromised by using a half radius overlap at the joints (center image). The code that actually creates the ODE bodies comprising the ragdoll is based around joint coordinates rather than limb lengths, and so the ragdoll can easily be modified to try out different amounts of overlap (the terminal endpoints defining the lengths of the head, hands, and feet will need slight adjustments because these endpoints are not actually joints, but simply positions chosen to produce the desired length capsule).

Different overlaps available for ragdoll joints.
Here are the body part lengths and derived joint coordinates; units are in meters. The ragdoll is defined in a standing position with arms straight out to the sides for easy setup of the ODE bodies, and facing down the positive Z-axis. Rotation matrices for each capsule are calculated automatically from the capsule's primary axis. Insert this code after the definition of makeOpenGLMatrix:
UPPER_ARM_LEN = 0.30 FORE_ARM_LEN = 0.25 HAND_LEN = 0.13 # wrist to mid-fingers only FOOT_LEN = 0.18 # ankles to base of ball of foot only HEEL_LEN = 0.05 BROW_H = 1.68 MOUTH_H = 1.53 NECK_H = 1.50 SHOULDER_H = 1.37 CHEST_H = 1.35 HIP_H = 0.86 KNEE_H = 0.48 ANKLE_H = 0.08 SHOULDER_W = 0.41 CHEST_W = 0.36 # actually wider, but we want narrower than shoulders (esp. with large radius) LEG_W = 0.28 # between middles of upper legs PELVIS_W = 0.25 # actually wider, but we want smaller than hip width R_SHOULDER_POS = (-SHOULDER_W * 0.5, SHOULDER_H, 0.0) L_SHOULDER_POS = (SHOULDER_W * 0.5, SHOULDER_H, 0.0) R_ELBOW_POS = sub3(R_SHOULDER_POS, (UPPER_ARM_LEN, 0.0, 0.0)) L_ELBOW_POS = add3(L_SHOULDER_POS, (UPPER_ARM_LEN, 0.0, 0.0)) R_WRIST_POS = sub3(R_ELBOW_POS, (FORE_ARM_LEN, 0.0, 0.0)) L_WRIST_POS = add3(L_ELBOW_POS, (FORE_ARM_LEN, 0.0, 0.0)) R_FINGERS_POS = sub3(R_WRIST_POS, (HAND_LEN, 0.0, 0.0)) L_FINGERS_POS = add3(L_WRIST_POS, (HAND_LEN, 0.0, 0.0)) R_HIP_POS = (-LEG_W * 0.5, HIP_H, 0.0) L_HIP_POS = (LEG_W * 0.5, HIP_H, 0.0) R_KNEE_POS = (-LEG_W * 0.5, KNEE_H, 0.0) L_KNEE_POS = (LEG_W * 0.5, KNEE_H, 0.0) R_ANKLE_POS = (-LEG_W * 0.5, ANKLE_H, 0.0) L_ANKLE_POS = (LEG_W * 0.5, ANKLE_H, 0.0) R_HEEL_POS = sub3(R_ANKLE_POS, (0.0, 0.0, HEEL_LEN)) L_HEEL_POS = sub3(L_ANKLE_POS, (0.0, 0.0, HEEL_LEN)) R_TOES_POS = add3(R_ANKLE_POS, (0.0, 0.0, FOOT_LEN)) L_TOES_POS = add3(L_ANKLE_POS, (0.0, 0.0, FOOT_LEN))
Finally we can create an initial version of a ragdoll by defining the RagDoll class. This version creates all of the capsule bodies and connects them with fixed and ball joints. Adding individual ODE bodies and creating each of these types of joints is handled by member functions allowing each capsule or joint to be created with a single command, and which eventually will augment some joints to allow for customized behavior. Note that the constructor takes an offset parameter which is a vector adjusting the position of the ragdoll, and is applied to every body and joint (another nice feature not included in this tutorial would be a rotation matrix so that a ragdoll can be created in any initial orientation as well as position). In the previously defined call to the constructor we create the ragdoll just under one meter above the floor. The class also contains an empty update member which will be filled in later. Insert this class directly below the joint position definitions:
class RagDoll(): def __init__(self, world, space, density, offset = (0.0, 0.0, 0.0)): """Creates a ragdoll of standard size at the given offset.""" self.world = world self.space = space self.density = density self.bodies = [] self.geoms = [] self.joints = [] self.totalMass = 0.0 self.offset = offset self.chest = self.addBody((-CHEST_W * 0.5, CHEST_H, 0.0), (CHEST_W * 0.5, CHEST_H, 0.0), 0.13) self.belly = self.addBody((0.0, CHEST_H - 0.1, 0.0), (0.0, HIP_H + 0.1, 0.0), 0.125) self.midSpine = self.addFixedJoint(self.chest, self.belly) self.pelvis = self.addBody((-PELVIS_W * 0.5, HIP_H, 0.0), (PELVIS_W * 0.5, HIP_H, 0.0), 0.125) self.lowSpine = self.addFixedJoint(self.belly, self.pelvis) self.head = self.addBody((0.0, BROW_H, 0.0), (0.0, MOUTH_H, 0.0), 0.11) self.neck = self.addBallJoint(self.chest, self.head, (0.0, NECK_H, 0.0)) self.rightUpperLeg = self.addBody(R_HIP_POS, R_KNEE_POS, 0.11) self.rightHip = self.addBallJoint(self.pelvis, self.rightUpperLeg, R_HIP_POS) self.leftUpperLeg = self.addBody(L_HIP_POS, L_KNEE_POS, 0.11) self.leftHip = self.addBallJoint(self.pelvis, self.leftUpperLeg, L_HIP_POS) self.rightLowerLeg = self.addBody(R_KNEE_POS, R_ANKLE_POS, 0.09) self.rightKnee = self.addBallJoint(self.rightUpperLeg, self.rightLowerLeg, R_KNEE_POS) self.leftLowerLeg = self.addBody(L_KNEE_POS, L_ANKLE_POS, 0.09) self.leftKnee = self.addBallJoint(self.leftUpperLeg, self.leftLowerLeg, L_KNEE_POS) self.rightFoot = self.addBody(R_HEEL_POS, R_TOES_POS, 0.09) self.rightAnkle = self.addBallJoint(self.rightLowerLeg, self.rightFoot, R_ANKLE_POS) self.leftFoot = self.addBody(L_HEEL_POS, L_TOES_POS, 0.09) self.leftAnkle = self.addBallJoint(self.leftLowerLeg, self.leftFoot, L_ANKLE_POS) self.rightUpperArm = self.addBody(R_SHOULDER_POS, R_ELBOW_POS, 0.08) self.rightShoulder = self.addBallJoint(self.chest, self.rightUpperArm, R_SHOULDER_POS) self.leftUpperArm = self.addBody(L_SHOULDER_POS, L_ELBOW_POS, 0.08) self.leftShoulder = self.addBallJoint(self.chest, self.leftUpperArm, L_SHOULDER_POS) self.rightForeArm = self.addBody(R_ELBOW_POS, R_WRIST_POS, 0.075) self.rightElbow = self.addBallJoint(self.rightUpperArm, self.rightForeArm, R_ELBOW_POS) self.leftForeArm = self.addBody(L_ELBOW_POS, L_WRIST_POS, 0.075) self.leftElbow = self.addBallJoint(self.leftUpperArm, self.leftForeArm, L_ELBOW_POS) self.rightHand = self.addBody(R_WRIST_POS, R_FINGERS_POS, 0.075) self.rightWrist = self.addBallJoint(self.rightForeArm, self.rightHand, R_WRIST_POS) self.leftHand = self.addBody(L_WRIST_POS, L_FINGERS_POS, 0.075) self.leftWrist = self.addBallJoint(self.leftForeArm, self.leftHand, L_WRIST_POS) def addBody(self, p1, p2, radius): """ Adds a capsule body between joint positions p1 and p2 and with given radius to the ragdoll. """ p1 = add3(p1, self.offset) p2 = add3(p2, self.offset) # cylinder length not including endcaps, make capsules overlap by half # radius at joints cyllen = dist3(p1, p2) - radius body = ode.Body(self.world) m = ode.Mass() m.setCappedCylinder(self.density, 3, radius, cyllen) body.setMass(m) # set parameters for drawing the body body.shape = "capsule" body.length = cyllen body.radius = radius # create a capsule geom for collision detection geom = ode.GeomCCylinder(self.space, radius, cyllen) geom.setBody(body) # define body rotation automatically from body axis za = norm3(sub3(p2, p1)) if (abs(dot3(za, (1.0, 0.0, 0.0))) < 0.7): xa = (1.0, 0.0, 0.0) else: xa = (0.0, 1.0, 0.0) ya = cross(za, xa) xa = norm3(cross(ya, za)) ya = cross(za, xa) rot = (xa[0], ya[0], za[0], xa[1], ya[1], za[1], xa[2], ya[2], za[2]) body.setPosition(mul3(add3(p1, p2), 0.5)) body.setRotation(rot) self.bodies.append(body) self.geoms.append(geom) self.totalMass += body.getMass().mass return body def addFixedJoint(self, body1, body2): joint = ode.FixedJoint(self.world) joint.attach(body1, body2) joint.setFixed() joint.style = "fixed" self.joints.append(joint) return joint def addBallJoint(self, body1, body2, anchor): anchor = add3(anchor, self.offset) # create the joint joint = ode.BallJoint(self.world) joint.attach(body1, body2) joint.setAnchor(anchor) joint.style = "ball" self.joints.append(joint) return joint def update(self): pass
Now you can run the script. Because of the heavy use of unconstrained ball joints the ragdoll will quickly collapse in jellyfish-like manner. In addition, each time the script is run the ragdoll collapses in exactly the same way. Note that the reported weight of the ragoll is about 170 lbs, a bit high (for being modeled after myself) despite using a low body density (ODE units are fairly arbitrary, but since I'm using metric a density of 1000 could mean 1000 kg/m3 which is the density of water, so a human should be about 900), but really close enough. Part of the discrepency is due to overlap between body parts which causes parts of the filled volume to have effectively doubled density, while the rest is attributable to the inexactness in representing a human body with a set of capsules. In any case we mostly care about the visual result here, not the precision of the physics.
To make things a bit more interesting let's add a small capsule placed at a random position under the ragdoll's feet. First we need to add some generic rotation matrices since we won't be using the automatic matrix calculation in RagDoll.addBody for lining up non-ragdoll bodies (only one of these matrices is actually used in this code, but the others might be useful for your own modifications). Insert this code after makeOpenGLMatrix:
# rotation directions are named by the third (z-axis) row of the 3x3 matrix, # because ODE capsules are oriented along the z-axis rightRot = (0.0, 0.0, -1.0, 0.0, 1.0, 0.0, 1.0, 0.0, 0.0) leftRot = (0.0, 0.0, 1.0, 0.0, 1.0, 0.0, -1.0, 0.0, 0.0) upRot = (1.0, 0.0, 0.0, 0.0, 0.0, -1.0, 0.0, 1.0, 0.0) downRot = (1.0, 0.0, 0.0, 0.0, 0.0, -1.0, 0.0, 1.0, 0.0) bkwdRot = (1.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 1.0)
Now add the randomly placed obstacle. Note that there is a commented out line setting the obstacle position directly; this is so you can recreate a previously run simulation by copying the obstacle position from that run which is printed to the console.
# create an obstacle obstacle, obsgeom = createCapsule(world, space, 1000, 0.05, 0.15) pos = (random.uniform(-0.3, 0.3), 0.2, random.uniform(-0.15, 0.2)) #pos = (0.27396178783269359, 0.20000000000000001, 0.17531818795388002) obstacle.setPosition(pos) obstacle.setRotation(rightRot) bodies.append(obstacle) print "obstacle created at %s" % (str(pos))

Ragdoll with only ball joints. Hey, it's a start.
Okay, so the ragdoll isn't any more realistic, but at the least the simulation is starting to get interesting. In the next section we'll start defining some simple but realistic joints that will make the ragdoll look a lot more human.
Adding Basic Joints
The simplest and most effective improvement we can make to the ragdoll is to add hinge joints. A hinge joint constrains rotation about a single axis, and ODE provides stops for hinge joints (among others) which limit rotations to a fixed range of angles, making hinge joints perfect for elbows and knees. We'll also use hinges for our ragdoll's wrists and ankles because hinges capture the most significant rotations possible with these joints, although for more realism you might instead use the universal joints discussed below.
First we will define the major coordinate axes available for rotation. There are six axes instead of three because for a hinge constrained by stops the direction (e.g., up versus down) matters because the rotation angles increase counter-clockwise around the hinge axis, and by defining complete anti-parallel axis pairs we can define left-right joint pairs using the same stop angles along and flipping only the rotation axis as needed. Add this code between the definitions of the primary rotation matrices and the ragdoll body dimensions:
# axes used to determine constrained joint rotations rightAxis = (1.0, 0.0, 0.0) leftAxis = (-1.0, 0.0, 0.0) upAxis = (0.0, 1.0, 0.0) downAxis = (0.0, -1.0, 0.0) bkwdAxis = (0.0, 0.0, 1.0) fwdAxis = (0.0, 0.0, -1.0)
Next, add the addHinge member to RagDoll after addFixedJoint. This function includes stop angle parameters which may be omitted to allow unrestricted rotation:
def addHingeJoint(self, body1, body2, anchor, axis, loStop = -ode.Infinity, hiStop = ode.Infinity): anchor = add3(anchor, self.offset) joint = ode.HingeJoint(self.world) joint.attach(body1, body2) joint.setAnchor(anchor) joint.setAxis(axis) joint.setParam(ode.ParamLoStop, loStop) joint.setParam(ode.ParamHiStop, hiStop) joint.style = "hinge" self.joints.append(joint) return joint
Now replace the code to create knee and ankle joints as ball joints with the following code creating hinge joints instead...
self.rightLowerLeg = self.addBody(R_KNEE_POS, R_ANKLE_POS, 0.09) self.rightKnee = self.addHingeJoint(self.rightUpperLeg, self.rightLowerLeg, R_KNEE_POS, leftAxis, 0.0, pi * 0.75) self.leftLowerLeg = self.addBody(L_KNEE_POS, L_ANKLE_POS, 0.09) self.leftKnee = self.addHingeJoint(self.leftUpperLeg, self.leftLowerLeg, L_KNEE_POS, leftAxis, 0.0, pi * 0.75) self.rightFoot = self.addBody(R_HEEL_POS, R_TOES_POS, 0.09) self.rightAnkle = self.addHingeJoint(self.rightLowerLeg, self.rightFoot, R_ANKLE_POS, rightAxis, -0.1 * pi, 0.05 * pi) self.leftFoot = self.addBody(L_HEEL_POS, L_TOES_POS, 0.09) self.leftAnkle = self.addHingeJoint(self.leftLowerLeg, self.leftFoot, L_ANKLE_POS, rightAxis, -0.1 * pi, 0.05 * pi)
...and similarly replace the code creating elbows and wrists:
self.rightForeArm = self.addBody(R_ELBOW_POS, R_WRIST_POS, 0.075) self.rightElbow = self.addHingeJoint(self.rightUpperArm, self.rightForeArm, R_ELBOW_POS, downAxis, 0.0, 0.6 * pi) self.leftForeArm = self.addBody(L_ELBOW_POS, L_WRIST_POS, 0.075) self.leftElbow = self.addHingeJoint(self.leftUpperArm, self.leftForeArm, L_ELBOW_POS, upAxis, 0.0, 0.6 * pi) self.rightHand = self.addBody(R_WRIST_POS, R_FINGERS_POS, 0.075) self.rightWrist = self.addHingeJoint(self.rightForeArm, self.rightHand, R_WRIST_POS, fwdAxis, -0.1 * pi, 0.2 * pi) self.leftHand = self.addBody(L_WRIST_POS, L_FINGERS_POS, 0.075) self.leftWrist = self.addHingeJoint(self.leftForeArm, self.leftHand, L_WRIST_POS, bkwdAxis, -0.1 * pi, 0.2 * pi)
Now rerun the simulation a few times. Things are looking a lot more realistic. Once in a while the ragdoll will collapse in ways that are barely distinguishable from a completed ragdoll, although the hips, shoulders, and neck all allow unrestricted rotation. More often the ragdoll will look like a human, albeit one which has just been pulled out of a horrific car crash.

Not perfect, but showing signs of improvement.
Next we want to add universal joints for the hips. Universal joints are basically just two perpendicular hinges combined into a single joint, allowing full pivoting while preventing twisting. Some ragdolls use universal joints for shoulders as well, as they are fairly simple to setup in ODE (simpler that the customized ball joints we're going to implement in the next section, anyways) and capture most of the desired rotation. On the other hand, for a super realistic ragdoll hips made from universal joints might actually be insufficient because real human hip joints are ball-and-sockets (like shoulders) which allow limited twisting in addition to pivoting. In this project I've decided that twisting is more important in the shoulders than in the hips, and so the hips are implemented using universal joints while the shoulders get customized ball joints.
I actually created the original shoulders using universal joints but had some stability problems. The arms would occasionally get caught behind the back or in other awkward positions which led to "spasms" that caused the ragdoll to move in unwanted ways. These problems were not entirely correctable with adjustments to the many ODE parameters governing collisions, stops, etc., but have not been an issue with the ragdoll's hip joints, presumably because the hips feature a more restricted range of motion. I'm also using an older version of ODE (0.5, because that's the version included with Kubuntu), so these stability problems may have since been fixed in more recent versions.
To implement the hips using universal joints, add this addUniversalJoint member to RagDoll after addHingeJoint:
def addUniversalJoint(self, body1, body2, anchor, axis1, axis2, loStop1 = -ode.Infinity, hiStop1 = ode.Infinity, loStop2 = -ode.Infinity, hiStop2 = ode.Infinity): anchor = add3(anchor, self.offset) joint = ode.UniversalJoint(self.world) joint.attach(body1, body2) joint.setAnchor(anchor) joint.setAxis1(axis1) joint.setAxis2(axis2) joint.setParam(ode.ParamLoStop, loStop1) joint.setParam(ode.ParamHiStop, hiStop1) joint.setParam(ode.ParamLoStop2, loStop2) joint.setParam(ode.ParamHiStop2, hiStop2) joint.style = "univ" self.joints.append(joint) return joint
Then replace the code creating the hip joints:
self.rightUpperLeg = self.addBody(R_HIP_POS, R_KNEE_POS, 0.11) self.rightHip = self.addUniversalJoint(self.pelvis, self.rightUpperLeg, R_HIP_POS, bkwdAxis, rightAxis, -0.1 * pi, 0.3 * pi, -0.15 * pi, 0.75 * pi) self.leftUpperLeg = self.addBody(L_HIP_POS, L_KNEE_POS, 0.11) self.leftHip = self.addUniversalJoint(self.pelvis, self.leftUpperLeg, L_HIP_POS, fwdAxis, rightAxis, -0.1 * pi, 0.3 * pi, -0.15 * pi, 0.75 * pi)
Running the simulation again shows more significant improvement. Because the ragdoll collapse depends more on the hips (which support half of the body) than the shoulders, things tend to look realistic until or unless the arms get caught underneath other parts of the body.

This guy looks great...from the chest down.
Enhancing the Ball Joints
The human body's shoulders are ball joints, and ODE has ball joints which we've already taken advantage of, so what's missing? ODE ball joints provide completely unrestricted rotation, while obviously the human shoulder restricts rotation quite a bit. There are two types of rotation we need to restrict which I call flex and twist. Briefly, flex is the amount the secondary body attached to the ball joint (the upper arm in the case of the shoulder joint) pivots away the joint's neutral direction, while twist is the amount the attached body rotates about its primary axis away from its neutral twist angle. By limiting flex we prevent the ragdoll's upper arm from being pulled all the way around its back, and by limiting twist we prevent the arm spinning like an axle.
To get a better feel for flex and the position of the neutral direction it is helpful to stick your arm straight out to the side. Rotating in the horizontal plane only you should be able to bright your arm most of the way across your chest at one extreme and pointing just a little bit to the back at the other. The component of the neutral direction lying within the horizontal plane is at the middle of these directions, just a bit outside of directly forwards. Vertically the range is a bit harder to gauge, but if you point your arms straight up there will likely be tension in your shoulder, while there is none hanging your arm straight down, though further rotation is effectively blocked by your torso. While vertical pivoting is practically unlimited the neutral direction should point slightly below horizontal to account for the tension with your arm pointed up.
Twist is best demonstrated with your elbow bent 90 degrees. Again stick your upper arm straight out to the side, but this time point your forearm forwards. You should be able to twist at the shoulder so your forearm points straight up, but probably not quite completely straight down (at least with your back straight), making the twist range about 180 degrees with the neutral twist angle of the upper arm defined (relative to itself through its own ODE rotation, which the forearm illustrates) by a vector perpendicular to the upper arm pointing just above horizontal with the ragdoll is in its initial arms out pose.
To restrict twist and flex in the ragdoll's shoulder joints we need to store in each joint the neutral direction (baseAxis) relative to the chest, while storing the natural up direction relative to both the chest (baseTwistUp) and the upper arm (baseTwistUp2). We also need to store soft angle limits for flex and twist, in addition to reactive torque magnitudes for pushing back when the joint rotations have exceeded the limits. In this implementation the shoulder joint does not act quite like ODE hinge and universal joints using hard stops because the reactive torque will not stop the joint from at least temporarily exceeding the angle limits, but this is actually desirable because with the shoulder a hard rotation threshold is a poor model for the gradually building resistive torque generated by muscle tension.
Before we update the ball joint creation code directly we need to add a utility function for transforming a vector from world coordinates into the local coordinate system of an ODE body, allowing the ball joint neutral direction and natural up direction to be stored relative to the bodies attached to the joints. Insert this code after makeOpenGLMatrix:
def getBodyRelVec(b, v): """ Returns the 3-vector v transformed into the local coordinate system of ODE body b. """ return rotate3(invert3x3(b.getRotation()), v)
Replace RagDoll.addBallJoint with the following version which takes neutral direction, angle limit, and resistive force parameters, and calculates and stores the neutral directions for the joint relative to the joined bodies:
def addBallJoint(self, body1, body2, anchor, baseAxis, baseTwistUp, flexLimit = pi, twistLimit = pi, flexForce = 0.0, twistForce = 0.0): anchor = add3(anchor, self.offset) # create the joint joint = ode.BallJoint(self.world) joint.attach(body1, body2) joint.setAnchor(anchor) # store the base orientation of the joint in the local coordinate system # of the primary body (because baseAxis and baseTwistUp may not be # orthogonal, the nearest vector to baseTwistUp but orthogonal to # baseAxis is calculated and stored with the joint) joint.baseAxis = getBodyRelVec(body1, baseAxis) tempTwistUp = getBodyRelVec(body1, baseTwistUp) baseSide = norm3(cross(tempTwistUp, joint.baseAxis)) joint.baseTwistUp = norm3(cross(joint.baseAxis, baseSide)) # store the base twist up vector (original version) in the local # coordinate system of the secondary body joint.baseTwistUp2 = getBodyRelVec(body2, baseTwistUp) # store joint rotation limits and resistive force factors joint.flexLimit = flexLimit joint.twistLimit = twistLimit joint.flexForce = flexForce joint.twistForce = twistForce joint.style = "ball" self.joints.append(joint) return joint
Next update the code adding the neck joint (which in addition to the shoulders also makes sense to model as a ball joint, given that it can pivot and twist, though the twisting isn't obvious when you're just looking at a capsule)...
self.neck = self.addBallJoint(self.chest, self.head, (0.0, NECK_H, 0.0), (0.0, -1.0, 0.0), (0.0, 0.0, 1.0), pi * 0.25, pi * 0.5, 50.0, 35.0)
...and of course, the shoulders:
self.rightUpperArm = self.addBody(R_SHOULDER_POS, R_ELBOW_POS, 0.08) self.rightShoulder = self.addBallJoint(self.chest, self.rightUpperArm, R_SHOULDER_POS, norm3((-1.0, -1.0, 4.0)), (0.0, 0.0, 1.0), pi * 0.5, pi * 0.25, 150.0, 100.0) self.leftUpperArm = self.addBody(L_SHOULDER_POS, L_ELBOW_POS, 0.08) self.leftShoulder = self.addBallJoint(self.chest, self.leftUpperArm, L_SHOULDER_POS, norm3((1.0, -1.0, 4.0)), (0.0, 0.0, 1.0), pi * 0.5, pi * 0.25, 150.0, 100.0)
So far, so good, though running the simulation at this point won't produce any different results than before because the built-in ODE ball joints aren't setup to make use of the additional joint information we've added. This is where RagDoll.update comes in. In this function, called during each ODE physics update step, we calculate first the current neutral vector for each ball joint by applying the current rotation of the primary body (e.g., the chest) to the stored vector, and then calculate the angle between this direction and the secondary body's (e.g., the upper arm) actual axis vector. If the angle is greater than the flex threshold we apply a counter torque with magnitude proportional to the excess rotation multiplied by the base flex force stored in the joint. Similarly, the neutral up direction is calculated and compared against the actual up direction, and if exceeded a counter torque is applied. The basic idea is quite simple, but all of the vector transforms and angle calculations, as well as tuning the base torque magnitudes, takes a fair amount of time to get right and offers several potential pitfalls.
One kind of important note: as coded this method violates conservation of angular momentum, one of the most sacred laws of physics. If this bothers you, simply apply the opposite torque(s) to the primary body as are applied to the secondary body. Otherwise don't sweat it, the simulation will probably look and work fine regardless. With that little matter brought to your attention, here is the code for update:
def update(self): for j in self.joints: if j.style == "ball": # determine base and current attached body axes baseAxis = rotate3(j.getBody(0).getRotation(), j.baseAxis) currAxis = zaxis(j.getBody(1).getRotation()) # get angular velocity of attached body relative to fixed body relAngVel = sub3(j.getBody(1).getAngularVel(), j.getBody(0).getAngularVel()) twistAngVel = project3(relAngVel, currAxis) flexAngVel = sub3(relAngVel, twistAngVel) # restrict limbs rotating too far from base axis angle = acosdot3(currAxis, baseAxis) if angle > j.flexLimit: # add torque to push body back towards base axis j.getBody(1).addTorque(mul3( norm3(cross(currAxis, baseAxis)), (angle - j.flexLimit) * j.flexForce)) # dampen flex to prevent bounceback j.getBody(1).addTorque(mul3(flexAngVel, -0.01 * j.flexForce)) # determine the base twist up vector for the current attached # body by applying the current joint flex to the fixed body's # base twist up vector baseTwistUp = rotate3(j.getBody(0).getRotation(), j.baseTwistUp) base2current = calcRotMatrix(norm3(cross(baseAxis, currAxis)), acosdot3(baseAxis, currAxis)) projBaseTwistUp = rotate3(base2current, baseTwistUp) # determine the current twist up vector from the attached body actualTwistUp = rotate3(j.getBody(1).getRotation(), j.baseTwistUp2) # restrict limbs twisting angle = acosdot3(actualTwistUp, projBaseTwistUp) if angle > j.twistLimit: # add torque to rotate body back towards base angle j.getBody(1).addTorque(mul3( norm3(cross(actualTwistUp, projBaseTwistUp)), (angle - j.twistLimit) * j.twistForce)) # dampen twisting j.getBody(1).addTorque(mul3(twistAngVel, -0.01 * j.twistForce))
Now rerun the simulation and voila! The ragdoll works as intended. While it can still collapse into some pretty interesting positions, they probably aren't anything you couldn't get into yourself with a bit of effort.
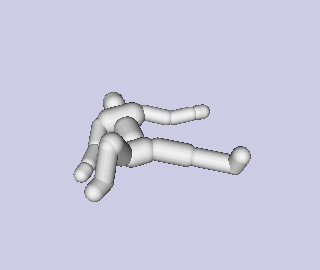
Yes, this is the picture of success in ragdoll land.
Contact me at arkaein@monsterden.net with any questions, or bug reports.