![\includegraphics[scale=0.5]{images/fig1quadtree.eps}](img8.png)
|
Author's Note: this paper was originally written in 2003 as part of a graduate level research project in Computer Science. I did not complete that graduate program (though I did later return to get my Master's in CS), and this paper never received the final improvements required for publication. I have decided to post it here in slightly reduced form so that whatever novel techniques it may contain may be shared with the community as was originally intended. Note that while the key technique described within was believed to be novel at the time of publication, as I have not kept up with the latest advances in the field of 3D surface registration over the past 7 years, it is quite possible similar techniques have been published in the interim. This paper is not intended to take credit away from any such authors in that situation.
Current methods for surface pair registration typically require fast pointcloud search techniques to identify exact nearest-neighbor vertex pairs between the surfaces. Although exact-point KD-trees offer fairly good performance at medium distances, surface pairs separated by larger distances incur severe performance penalties using these methods. This article presents alternative nearest-neighbor search techniques using Barnes-Hut trees and approximation KD-trees to estimate the location of the nearest point on a surface with time complexity unaffected by search distance. Although these structures provide approximate nearest-neighbors rather than exact results like standard search trees, the precision of the approximation increases for search points closest to the target surface, making them ideal for surface registration. Though Barnes-Hut trees and approximation KD-trees both provide viable solutions, Barnes-Hut trees are favored due to smaller tree height than analogous KD-trees, offering slightly shorter mean time to estimate a nearest-neighbor.
3D surface registration is widely used in computer graphics, computer vision, and scientific and engineering applications. Specific problems requiring registration methods include reconstruction of complete 3D models from partial images, and identifying similar or matching objects in various positions and orientations. The methods discussed in this paper were developed for registration of dental images for quantitative analysis, but can be applied to applications such as CAD/CAM reconstruction and reverse engineering.
Proven methods for 3D surface registration involve iterated processes seeking to minimize distances between neighboring vertex pairs between two pointclouds. The basic method for building a set of associated vertex pairs is to find the nearest vertex in the target surface for each vertex in the base surface. Traditional methods for identifying nearest vertex pairs include building search trees and projecting points onto 2D surface meshes [3]. Least squares or quaternion based optimization methods methods are used to minimize the distances between vertex pairs [13], [7], [15]. This process of identifying matching pairs and minimizing distances is iterated until the surfaces are optimally aligned.
Most of the processing required for the algorithm is spent identifying nearest vertex pairs between the two surfaces. The most robust methods for locating nearest vertices within arbitrary distance thresholds utilize searchable trees, typically KD-trees decomposing the pointcloud geometrically. Optimal heuristic search algorithms identify the point nearest to a 3D position quickly if the search is limited to a small radius around the target or the nearest point is very close to the target position, but require many more steps to identify the nearest point for large search radii when separated by relatively large distances.
![\includegraphics[scale=0.5]{images/fig1quadtree.eps}](img8.png)
|
Figure 1 shows how a quadtree decomposes a small pointcloud in 2D. Specialized tree structures can drastically reduce execution time for nearest-neighbor search by approximating the surface point nearest to the 3D target coordinates. The approximation structures discussed in this paper are Barnes-Hut trees, originally developed for solving N-body problems in astronomy [1], as well as KD-trees augmented with similar capabilities. Rather than simply decomposing a pointcloud down to its constituent points, the approximation trees discussed in this paper store the centroid coordinates of vertex subsets at each level of decomposition, providing an approximation of a localized portion of the represented surface that increases in accuracy as the subvolume point count decreases deeper in the tree. A simple depth first search without need for backtracking typically used in standard tree search algorithms quickly determines the smallest subvolume containing the search coordinates. The closer the search coordinates are to an actual vertex the more precise the approximation is likely to be. Although a small proportion of nearest-point calculations are sure to be inaccurate when using approximation methods, it will be shown that average precision over the entire surface is completely sufficient for excellent registration.
The standard algorithm for the registration of two 3D surfaces is the Iterating Closest Point algorithm [2] developed by Besl and McKay. The general algorithm is designed to work for all common surface and curve representations including pointclouds, triangle meshes and parametric curves and surfaces, in any combination. In this paper we are concerned with regularly spaced pointclouds which lend themselves naturally to nearest-neighbor approximation methods. This type of pointcloud is most useful in scientific and engineering applications. The ICP algorithm specialized for 3D pointclouds aligns two surfaces by minimizing the sum of squared distances between nearest vertex pairs between the surfaces. The registration is completed when the change in vertex pair root-mean-square (RMS) distance between iterations falls below a selected threshold. The basic algorithm is:
function ICP(A, B, MaxSteps, DeltaRMS)

In this algorithm ![]() is the fixed surface and
is the fixed surface and ![]() is the movable surface.
FindNearVertex() is a function that identifies the nearest point on
surface
is the movable surface.
FindNearVertex() is a function that identifies the nearest point on
surface ![]() to vertex
to vertex ![]() . Align() calculates the rigid
transformation for the points in
. Align() calculates the rigid
transformation for the points in ![]() that minimizes the sum of squared
distances to the corresponding nearest-neighbors stored in
that minimizes the sum of squared
distances to the corresponding nearest-neighbors stored in ![]() and applies
this transformation to
and applies
this transformation to ![]() .
. ![]() and
and ![]() are user defined settings
that limit the amount of computation spent on the registration process to
balance algorithm run-time with registration precision.
are user defined settings
that limit the amount of computation spent on the registration process to
balance algorithm run-time with registration precision.
Several enhancements have been made to this basic algorithm, many of which
apply specifically to the FindNearVertex() function. A fairly
complete roundup of these ICP variants have been examined by Rusinkiewicz and
Levoy [11]. The original ICP algorithm placed no limit on the distance
between nearest points, requiring that the surface ![]() is actually a subset of
surface
is actually a subset of
surface ![]() to prevent spurious pairings. Recent implementations usually employ
a hard threshold to discard vertex pairs separated by more than a particular
fixed distance. Chen and Medioni extended the surface normal associated with the
point
to prevent spurious pairings. Recent implementations usually employ
a hard threshold to discard vertex pairs separated by more than a particular
fixed distance. Chen and Medioni extended the surface normal associated with the
point ![]() on surface
on surface ![]() until it intersected the plane tangent to the nearest
point
until it intersected the plane tangent to the nearest
point ![]() on
on ![]() . Point
. Point ![]() is replaced by this calculated point
[4]. This approach prevents surfaces getting stuck due to arbitrary
vertex associations along relatively flat surface regions, particularly for
pointclouds sampled at regular mesh intervals. The results of point-plane
estimation are similar to what can be achieved by finding the nearest point on a
triangulated mesh but with greater speed. Dorai et. al. incorporated sensor
inaccuracies inherent in range data acquisition into the calculations of the
tangent plane [5]. Masuda et. al. proposed using a soft distance
threshold such that only the nearest
is replaced by this calculated point
[4]. This approach prevents surfaces getting stuck due to arbitrary
vertex associations along relatively flat surface regions, particularly for
pointclouds sampled at regular mesh intervals. The results of point-plane
estimation are similar to what can be achieved by finding the nearest point on a
triangulated mesh but with greater speed. Dorai et. al. incorporated sensor
inaccuracies inherent in range data acquisition into the calculations of the
tangent plane [5]. Masuda et. al. proposed using a soft distance
threshold such that only the nearest ![]() of pairs found each iteration were
used for the least squares calculation [8]. While various methods
may be used to determine
of pairs found each iteration were
used for the least squares calculation [8]. While various methods
may be used to determine ![]() , Masuda set it relative to the proportion of
overlap calculated between the surfaces. Soft thresholds can be more appropriate
than hard thresholds in situations where the average distance between
nearest-neighbor points on the surfaces is not previously known. Soft thresholds
have also been used in conjunction with hard thresholds, where coarse
adjustments are made with large hard thresholds and small soft thresholds, with
finer adjustments progressively decreasing the hard threshold and increasing the
soft threshold [10].
, Masuda set it relative to the proportion of
overlap calculated between the surfaces. Soft thresholds can be more appropriate
than hard thresholds in situations where the average distance between
nearest-neighbor points on the surfaces is not previously known. Soft thresholds
have also been used in conjunction with hard thresholds, where coarse
adjustments are made with large hard thresholds and small soft thresholds, with
finer adjustments progressively decreasing the hard threshold and increasing the
soft threshold [10].
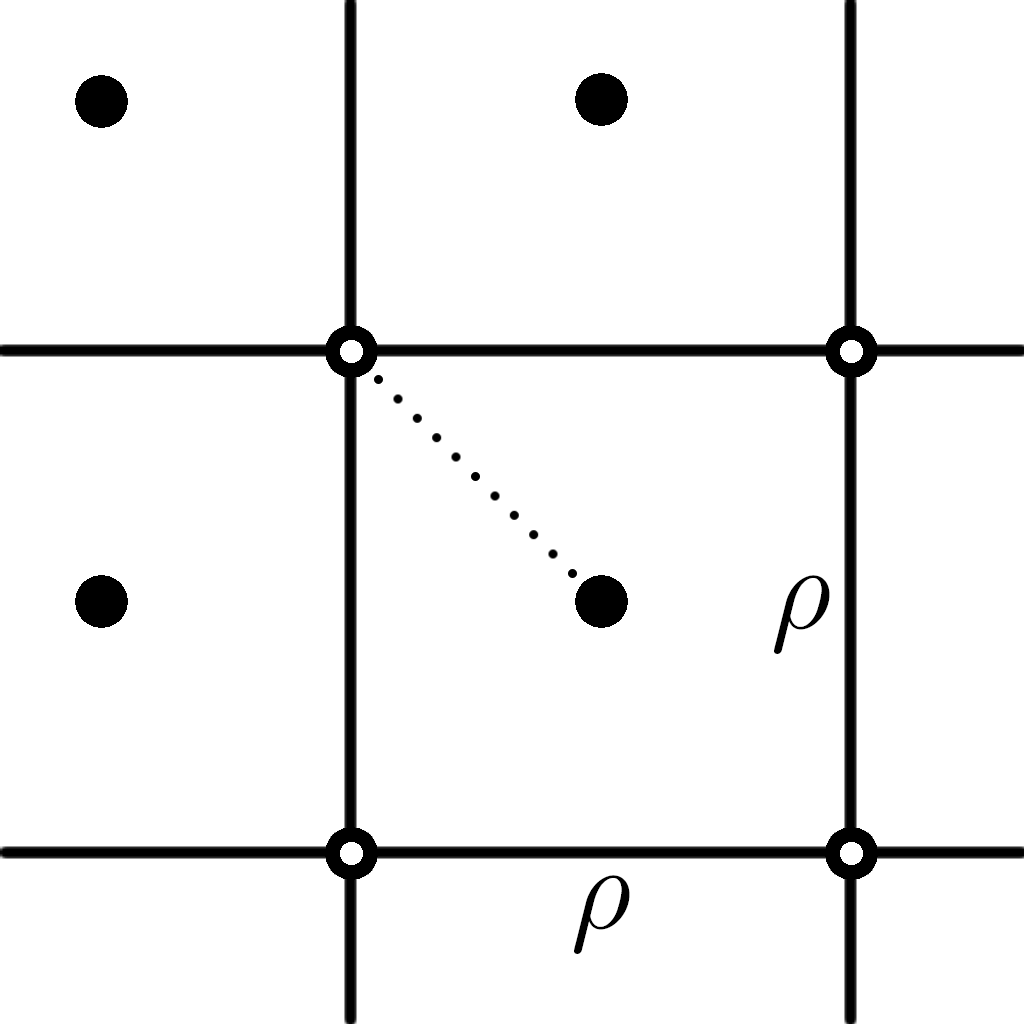
Several methods have been proposed to eliminate bad pairings on surface boundaries. With partially overlapping surfaces, vertices in non-overlapping sections of one surface will pair with boundary vertices on the other surface (Figure 2). Turk and Levoy marked all boundary points on the target surface and discarded any pairs which included one [14]. Other bad pair elimination heuristics include placing a threshold on the maximum angle between pair normal vectors [6].
![\includegraphics[scale=0.5]{images/fig3badpair.eps}](img17.png)
|
Finally, there are several enhancements to the ICP algorithm that seek to
maximize speed. Besl and McKay implemented ICP with acceleration. When
a consecutive set of iterations improve the registration while moving in roughly
the same direction, the registration is accelerated by predicting the final
local minimum of the registration. The registration vector curve tends to follow
a parabola in 7 space, so three consecutive iterations are required to
extrapolate the point on the parabola minimizing RMS distance between the
surfaces [2]. The accelerated ICP was improved by Simon by uncoupling
the translation and rotation acceleration [12]. Simon also introduced
nearest-neighbor caching. For each point in the search set, the nearest ![]() points are found in one shot. These points are cached until the starting point
in the movable model moves far enough relative to the distance between
the closest and farthest cached points that the set needs to be updated.
points are found in one shot. These points are cached until the starting point
in the movable model moves far enough relative to the distance between
the closest and farthest cached points that the set needs to be updated.
Because this paper primarily analyzes the speed of nearest-neighbor search algorithms none of these enhancements have been implemented for the experimental testing, however these methods are recommended for implementations requiring maximum performance.
The most fundamental operation in consideration of the performance of the ICP
algorithm is identifying nearest-neighbor points between surfaces, due to the
large potential number of points defining a high-resolution surface. Standard
nearest point search methods typically utilize search trees. In general, search
trees of ![]() points can locate the point nearest to a search position in
approximately
points can locate the point nearest to a search position in
approximately ![]() time, as long as it is assumed the search distance is
small relative to the pointcloud dimensions (this assumption is held for the
applications described in this paper).
time, as long as it is assumed the search distance is
small relative to the pointcloud dimensions (this assumption is held for the
applications described in this paper).
The implementation of search structures depends greatly on the type of organization used in the pointcloud. The software used for this paper utilizes voxel grids. A voxel is the 3D analogy to the 2D pixel, breaking up space into discretized units such that any 3D point with real coordinates can be mapped to a voxel with integer coordinates. In the experiments for this paper all pointclouds are stored on voxel grids with no more than one point per voxel. The voxel grid combined with the one-to-one mapping of points to voxels simplifies the creation of KD-trees. In implementations designed to maximize speed, performance during the search may be improved by using the integer voxel coordinates. In particular, these constraints guarantee that search coordinates within a voxel containing a surface vertex will evaluate that vertex as the nearest-neighbor for all search methods, whether exact or approximating. This does not guarantee the evaluated vertex is actually the closest to the search coordinates, but it is typically the case.
Slight inaccuracies may occur in determining nearest-neighbors in different voxels than the search coordinates. In general, the vertex calculated nearest to a 3D point should be identical across all search methods for a given search distance tolerance. However, as Figure 3 demonstrates, with integer coordinates there will be many situations in which two or more nearby voxel coordinates will be equally close. Different search methods will be biased towards different points in such situations. For relatively flat regions on typical surfaces, these slight biases in nearest-point calculation are of little consequence when estimation methods such as point-plane are used because the interpolation will yield very similar results for all of the neighboring points, and so should have little impact on overall registration precision. Regions with greater curvature may produce greater approximation errors, however they will still be acceptable in most situations, as the experimental data will show.
![\includegraphics[scale=0.375]{images/fig4nearvoxel.eps}](img20.png)
|
For the remainder of this paper the following convention will be used to
describe search parameters. Because the search implementations discussed are
focused on pointclouds organized on voxel grids, the primary search parameter is
the voxel search range
![]() , where
, where ![]() is the
maximum search distance tolerance and
is the
maximum search distance tolerance and ![]() is the voxel side length. The point
count for the target pointcloud will be
is the voxel side length. The point
count for the target pointcloud will be ![]() . In cases where the bounding volume
of the pointcloud is concerned,
. In cases where the bounding volume
of the pointcloud is concerned, ![]() will denote the maximum dimensions in voxels
of the 3D bounding box for the pointcloud.
will denote the maximum dimensions in voxels
of the 3D bounding box for the pointcloud.
KD-trees subdivide pointclouds into roughly equal numbers by planes
perpendicular to one of the coordinate axes in 3D space. Ensuring the tree is
balanced determines the height of the tree to be ![]() . The major
benefit KD-trees offer over other decomposition methods is a minimal amount of
branching. The search algorithm used with KD-trees to determine the nearest
point must evaluate all branches along every node from the root to the nearest
point. Branches not evaluated immediately are sorted into a queue by ascending
minimum expected error of the best possible point in the subtree. If there is a
point in the tree at the exact voxel coordinates specified the algorithm will
need to evaluate approximately
. The major
benefit KD-trees offer over other decomposition methods is a minimal amount of
branching. The search algorithm used with KD-trees to determine the nearest
point must evaluate all branches along every node from the root to the nearest
point. Branches not evaluated immediately are sorted into a queue by ascending
minimum expected error of the best possible point in the subtree. If there is a
point in the tree at the exact voxel coordinates specified the algorithm will
need to evaluate approximately ![]() nodes. Other searches will evaluate
all nodes that may lead to a point within the search volume that could be closer
than the closest point found by that time in the search process.
nodes. Other searches will evaluate
all nodes that may lead to a point within the search volume that could be closer
than the closest point found by that time in the search process.
There are several minor variations on the basic KD-tree structure. Simpler implementations may always divide the points using a plane perpendicular to the X-axis first, then the Y-axis, then Z, and so on, repeated until all subvolumes contain only a single point. This method is fairly effective but does not take full advantage of the unique topology of each pointcloud. It is also possible to create a KD-tree by inserting points one at a time, passing the new point down the existing branches of tree until a leaf is reached, which is then split into two new branches containing the original leaf point and the new leaf point. This method may lead to very unbalanced trees unless the order in which the points are inserted is carefully chosen. For the experiments performed for this paper a more sophisticated KD-tree implementation was chosen. The point set is subdivided at the median point along its longest coordinate dimension, yielding a well balanced tree with interior nodes covering the most compact possible volumes. The tradeoff for improved search performance is slightly increased processing required to build the KD-tree.
Similar to KD-trees, octrees subdivide a pointcloud into a hierarchy of volumes. Octrees are constructed by recursively subdividing a rectangular parallelepiped enclosing the pointcloud and with faces perpendicular to the three coordinate axes into eight subvolumes until each contains only a single point. Octrees are wider and shorter than KD-trees, generally with shorter paths from root to leaf but with more branches to consider at each node. Octrees are searched for nearest points using an algorithm very similar to that used for KD-trees, requiring a queue to store potential search nodes. Octrees are generally inferior to KD-trees for single nearest-point search, however they are included here for completeness in that they blend the exact point qualities of KD-trees and the overall structure of Barnes-Hut trees, discussed in the next section.
As with KD-trees, octrees have many subtle variations. Generalized octrees have
unrestricted depth which will vary in proportion with the regional density of the
pointcloud. This may lead to inefficient, unbalanced trees. A solution to
varying density is dynamic subdivision, similar to the median-based partitioning
used with KD-trees. This approach is uncommon due to the difficulties in
efficiently choosing the optimal positions of the three dividing planes for each
interior node volume compared with the relatively simple median calculation for
KD-trees. For the experiments in this paper a more basic model was used suitable
to the ordered voxel arrangement of the pointclouds tested. The initial volume of
the octree is the cube with dimensions ![]() centered at the midpoint voxel
coordinates of the pointcloud, for which
centered at the midpoint voxel
coordinates of the pointcloud, for which
![]() , where
, where ![]() is
an integer power and
is
an integer power and ![]() is the maximum length, in voxels, of the pointcloud
bounding box.
is the maximum length, in voxels, of the pointcloud
bounding box.
Barnes-Hut trees augment an otherwise typical octree by storing in each node the weighted average of the vertex coordinates (and optionally the surface normal vectors) of the points in the subtree of that node. Because this augmentation does not affect the general structure, Barnes-Hut trees come in variations similar to octrees. They traditionally use simple cubic decomposition but may use dynamic methods with non-cubic rectangular parallelepipeds. For voxel organization, as in the implementations for this paper, cubic decomposition is the obvious choice.
A convenient property of Barnes-Hut trees is that because each node contains an average of vertex coordinates it is not necessary to ensure that each point is stored in its own leaf node. For pointclouds of variable density the maximum height of the tree can be capped by setting an arbitrary minimum resolution that may be completely independent of the typical or average distance between neighboring points. Though undetermined tree height is not an issue for pointclouds organized on voxel grids a Barnes-Hut tree resolution coarser than the voxel resolution may be chosen to generate a smaller, faster performing tree when maximum precision is not necessary. Similar approaches for standard point octrees may necessitate choosing a single point, possibly arbitrarily, to represent a local group, which is likely to be less representative of the group than the coordinate average.
The creation of a Barnes-Hut tree is similar to standard octree creation. The
voxel boundaries of the pointcloud are determined and an initial cubic volume
with side length ![]() (see above) is centered on the midpoint voxel
coordinates. Points are added one at a time, with each node along the path from
the root node to the leaf adding the point coordinates to the node's weighted
sum. For simplicity the implementation used in this paper creates the branch
nodes all the way down to the bottom level of the tree regardless of whether the
intermediate nodes contain any other points. For slightly lower memory costs and
slightly faster performance nodes may be built only until the maximum allowed
depth is reached or the current inserted point resides in its own node. If
another point is inserted that must share this interior node the node can then
be split into two new leaves. Alternatively the tree may be constructed the
first way with all redundant nodes trimmed at the end. After every point has
been inserted the coordinates at each node are divided by the number of points
inserted through the node.
(see above) is centered on the midpoint voxel
coordinates. Points are added one at a time, with each node along the path from
the root node to the leaf adding the point coordinates to the node's weighted
sum. For simplicity the implementation used in this paper creates the branch
nodes all the way down to the bottom level of the tree regardless of whether the
intermediate nodes contain any other points. For slightly lower memory costs and
slightly faster performance nodes may be built only until the maximum allowed
depth is reached or the current inserted point resides in its own node. If
another point is inserted that must share this interior node the node can then
be split into two new leaves. Alternatively the tree may be constructed the
first way with all redundant nodes trimmed at the end. After every point has
been inserted the coordinates at each node are divided by the number of points
inserted through the node.
Barnes-Hut search is trivial. The tree is traversed depth-first until the deepest node containing the voxel search coordinates is reached (the root node may be used if the search coordinates are outside of the tree boundaries, though the resulting approximated point will almost surely be discarded as being too far from the search coordinates). The nearest-neighbor surface point approximation is set to the coordinate average stored at this node. If the pointcloud contains a point at the voxel search coordinates this point will be set and the results will be the same as for an exact point search (as long as there is only one point per voxel). Otherwise the result is an average of points in the local spatial region.
A potential benefit of Barnes-Hut trees to be mentioned but not explored further in this paper is that of point weighting. There are many situations where it may be useful to favor certain points over others in registration. When dealing with point data acquired using range laser scanners mesh boundary points typically appear closer than their neighbors [14]. Additionally, the greater the angle between the sensor and vector normal to the surface the less reliable the coordinate calculation [14], [6]. The ICP algorithm can be adapted to give more influence to points with higher weights. Isolated points with small weights will have small influence in the registration, or may simply be culled from the Barnes-Hut tree altogether. Other structures could store these vertex weights, but the inherent averaging of Barnes-Hut trees means that low-weighted points at the same voxel coordinates can be combined to form a single, stronger point.
As Barnes-Hut tree structures match standard octree structures, approximation KD-trees are structured much like any other KD-tree. Different decomposition methods are available, with tradeoffs being creation time and code complexity versus search efficiency. The implementation described here used the same longest-median division method used with exact-point KD-trees. Like Barnes-Hut trees, approximation KD-trees share the potential advantages of the ability to set arbitrary voxel resolutions to conserve memory. They may also include the same manner of weighted averaging to limit the influence of unreliable singular points
Approximation KD-trees are constructed much the same as any KD-tree. The pointcloud is recursively subdivided along the longest dimension, with each internal node storing the average coordinates of its set of points. Unlike the described Barnes-Hut tree implementation no secondary weight scaling step is needed because the pointcloud is always (in optimal implementations) decomposed rather than inserted one point at a time.
Nearest-neighbor approximation is as simple as for Barnes-Hut trees. Depth first search locates the lowest node in the tree defining a volume containing the voxel search coordinates. These coordinates are evaluated as the nearest surface point approximation.
When evaluating the relative effectiveness of various search methods we are primarily concerned with worst-case performance, for two reasons. The first is that many surface pairs that are registered have significant non-overlapping regions. The larger the search distance, the more these non-overlapping points form spurious pairings only to be discarded by later vertex pair tests, as described in Section 2. The second reason is that in most well configured surface registrations the search algorithm will push the limits of the set distance tolerance. If the tolerance is set significantly higher than the average distance between the surfaces at the beginning of the registration process it will negatively impact both the speed and precision of the algorithm. This is true even for the approximation structures for which search time is unaffected by distance tolerance. Because greater search distance means an increased number of vertex pairs to evaluate, the probability of mismatched vertex pairs increases as search distance increases.
Generally speaking expected search time for KD-trees and octrees as used in the
ICP algorithm described here is ![]() [15], [6].
More detailed analysis is dependent upon the search range relative to tree
resolution. With average height of
[15], [6].
More detailed analysis is dependent upon the search range relative to tree
resolution. With average height of ![]() , KD-trees with small search
ranges (
, KD-trees with small search
ranges (![]() ) are capable of time complexity approaching
) are capable of time complexity approaching ![]() .
Similarly, octree search with small values of
.
Similarly, octree search with small values of ![]() is capable of
close to
is capable of
close to ![]() worst-case complexity. As
worst-case complexity. As ![]() increases the analysis
becomes more difficult. The time required to execute a search examining
increases the analysis
becomes more difficult. The time required to execute a search examining ![]() nodes is
nodes is ![]() . The minimum worst-case value of
. The minimum worst-case value of ![]() for any search is the
number of points within the search range. Though this could theoretically be
for any search is the
number of points within the search range. Though this could theoretically be
![]() for a noisy or wavy surface that fills the local volume, for a typical
manifold surface it is more likely in the neighborhood of
for a noisy or wavy surface that fills the local volume, for a typical
manifold surface it is more likely in the neighborhood of ![]() . Of course this
only considers the leaf nodes, all parents of these nodes must be examined.
Trees with high branching factor generally have fewer parent nodes for a group
of localized leaf nodes. However, for each parent node that may contain a
descendent within the search range, every immediate child which cannot contain a
leaf node within the range must be examined before being discarded, in which
case high branching factor works against efficiency, and makes the time analysis
even murkier. Suffice it to say that for typical 3D surface pointclouds the time
complexity for intermediate search ranges is close to
. Of course this
only considers the leaf nodes, all parents of these nodes must be examined.
Trees with high branching factor generally have fewer parent nodes for a group
of localized leaf nodes. However, for each parent node that may contain a
descendent within the search range, every immediate child which cannot contain a
leaf node within the range must be examined before being discarded, in which
case high branching factor works against efficiency, and makes the time analysis
even murkier. Suffice it to say that for typical 3D surface pointclouds the time
complexity for intermediate search ranges is close to
![]() , as
the tree search will never be significantly slower than the brute force search,
and in almost all cases should be significantly faster, even with infinite
search range.
, as
the tree search will never be significantly slower than the brute force search,
and in almost all cases should be significantly faster, even with infinite
search range.
In cases where especially large pointclouds are registered, efficient memory
usage may be as important as raw speed. Therefore, discussion of the relative
memory requirements of the search structures is in order. Table
1 shows the estimated memory requirements for the
implementations used in experimentation. The calculations are based on estimated
stored node count for each structure as a function of point count and
unit node size in bytes. For octrees and KD-trees the number of stored nodes is
less than the number of expected nodes because the leaf nodes are encapsulated
within the parent node data. The structures were designed to maximize memory efficiency for
pointclouds with anywhere from several hundred to several million points and
voxel dimensions up to ![]() (over 6 meters at
(over 6 meters at ![]() resolution).
resolution).
From the table, the point-indexing tree structures offer the smallest memory
cost. A KD-tree always has exactly ![]() nodes, including the leaves. The
number of nodes in an octree cannot be determined as precisely from the number
of points; however, for sufficiently large pointclouds representing typical
manifold surfaces, the number of nodes is about
nodes, including the leaves. The
number of nodes in an octree cannot be determined as precisely from the number
of points; however, for sufficiently large pointclouds representing typical
manifold surfaces, the number of nodes is about ![]() , as observed across a
large set of reconstructed 3D models containing tens to hundreds of thousands of
points. The implementation used here eliminates the need to use actual leaf
nodes by storing each point index in the memory normally used to reference
interior tree nodes, reducing the actual stored node count for KD-trees and
octrees by
, as observed across a
large set of reconstructed 3D models containing tens to hundreds of thousands of
points. The implementation used here eliminates the need to use actual leaf
nodes by storing each point index in the memory normally used to reference
interior tree nodes, reducing the actual stored node count for KD-trees and
octrees by ![]() .
.
The approximation tree structures require the largest amount of memory because they store point (and in some cases normal vector) averages rather than indices and because the leaves require actual nodes. The high branching factor of octrees compared with KD-trees gives Barnes-Hut trees an advantage over approximation KD-trees due to the smaller number of interior (and therefore total) nodes.
| Structure | No. of Nodes | Node Size | Est. Total Size |
| KD-Tree | 33 | ||
| Octree | 32 | ||
| Barnes-Hut Tree | 40 | ||
| Approx. KD-Tree | 49 |
To compare surface registration utilizing different search methods, each
method was tested against an overlapping surface pair with various combinations
of relative starting orientations and search distance tolerances.
To ensure perfect overlap between the test surfaces, each was extracted as
overlapping sections of a larger surface from a digitized dental lower jaw
model.
Six different initial orientations (including perfect
registration) were tested using different combinations of translations and
rotations of various magnitudes. Five different search distance tolerances were
used starting with ![]() (one-half the pointcloud voxel side length) and
increasing by successive powers of two to a maximum distance of
(one-half the pointcloud voxel side length) and
increasing by successive powers of two to a maximum distance of ![]() .
Aggregate results for each search method were then compared. The complete set of
test configurations is shown in Table 2. Performance is
evaluated by three metrics: effectiveness, execution time and number of
iterations until convergence.
.
Aggregate results for each search method were then compared. The complete set of
test configurations is shown in Table 2. Performance is
evaluated by three metrics: effectiveness, execution time and number of
iterations until convergence.
| No. | RX | RY | RZ | TX | TY | TZ |
| 1 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 |
| 2 | 1.0 | 1.0 | 1.0 | 0 | 0 | 0 |
| 3 | 2.0 | 2.0 | 2.0 | 0 | 0 | 0 |
| 4 | 0.0 | 0.0 | 0.0 | 500 | 250 | 250 |
| 5 | 0.0 | 0.0 | 0.0 | 1000 | 500 | 500 |
| 6 | 1.0 | 2.0 | 1.0 | 500 | 1000 | 500 |
Effectiveness of surface registration can be difficult to measure quantitatively. A simple measurement is the RMS distance between nearest-neighbor vertex pairs between the surfaces, discarding pairs that are not a good match by the same criteria used during registration. This works well if the registration is at least moderately successful. It works poorly for unsuccessful registration due to lack of vertex pairs representing actual corresponding surface features. Because this experiment used overlapping sections taken from a single surface all corresponding vertex pairs between the sections were easily identified while in perfect registration. This allows RMS distance after convergence to serve as an excellent registration metric.
Execution time, measured in seconds, includes the registration process only. It does not include the time required to build necessary search structures because these structures are typically created once for each surface and used for multiple algorithms during the execution of an application. The number of iterations necessary is also straightforward. For the implementation used here, the registration process stops after 25 iterations of no improvement in current registration. The algorithm will stop sooner only if absolute convergence is reached, i.e. the position of the moving surface does not change between consecutive iterations (either because of apparently perfect registration or zero vertex pairs found).
Ideally, every exact point search method would locate the same nearest point given a search position and maximum distance tolerance. Unfortunately, there may be situations where there are two points at equal distances such that the nearest point found is determined to be the point evaluated first by the particular search algorithm. Using exact coordinate distances this situation would occur no more than a handful of times out of a thousand for typical real world data. Using voxel coordinates means it occurs much more often, and there will be slight variations in the final registration for each method. Specifically, this will be seen in nearest-neighbor RMS distance and number of iterations for each test configuration for algorithms other than the Barnes-Hut and the KD-tree approximations. The approximation methods differ even more significantly from these methods, and from each other.
|
|
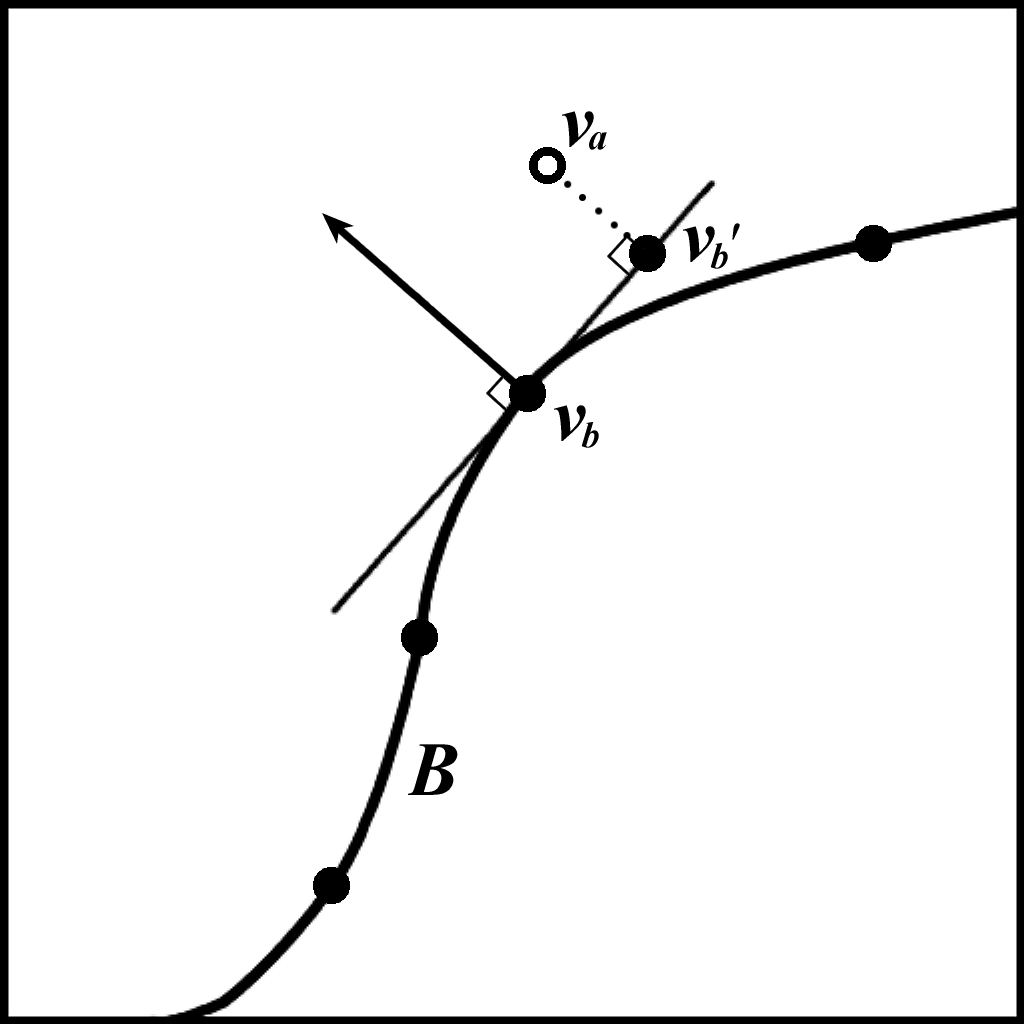
The ICP implementation for the experiments in this paper used a slightly
modified version of Chen and Medioni's point-plane method [4] to
determine the movable surface point closest to the nearest vertex found on the
fixed surface. Instead of extending the normal of point ![]() , the plane tangent
to
, the plane tangent
to ![]() is calculated, then
is calculated, then ![]() is replaced by the point on this plane
closest to the nearest neighbor
is replaced by the point on this plane
closest to the nearest neighbor ![]() (Figure 4). This method
only requires the normal vectors on surface
(Figure 4). This method
only requires the normal vectors on surface ![]() to be known. A hard distance
threshold was set for all iterations, with surface distance measured
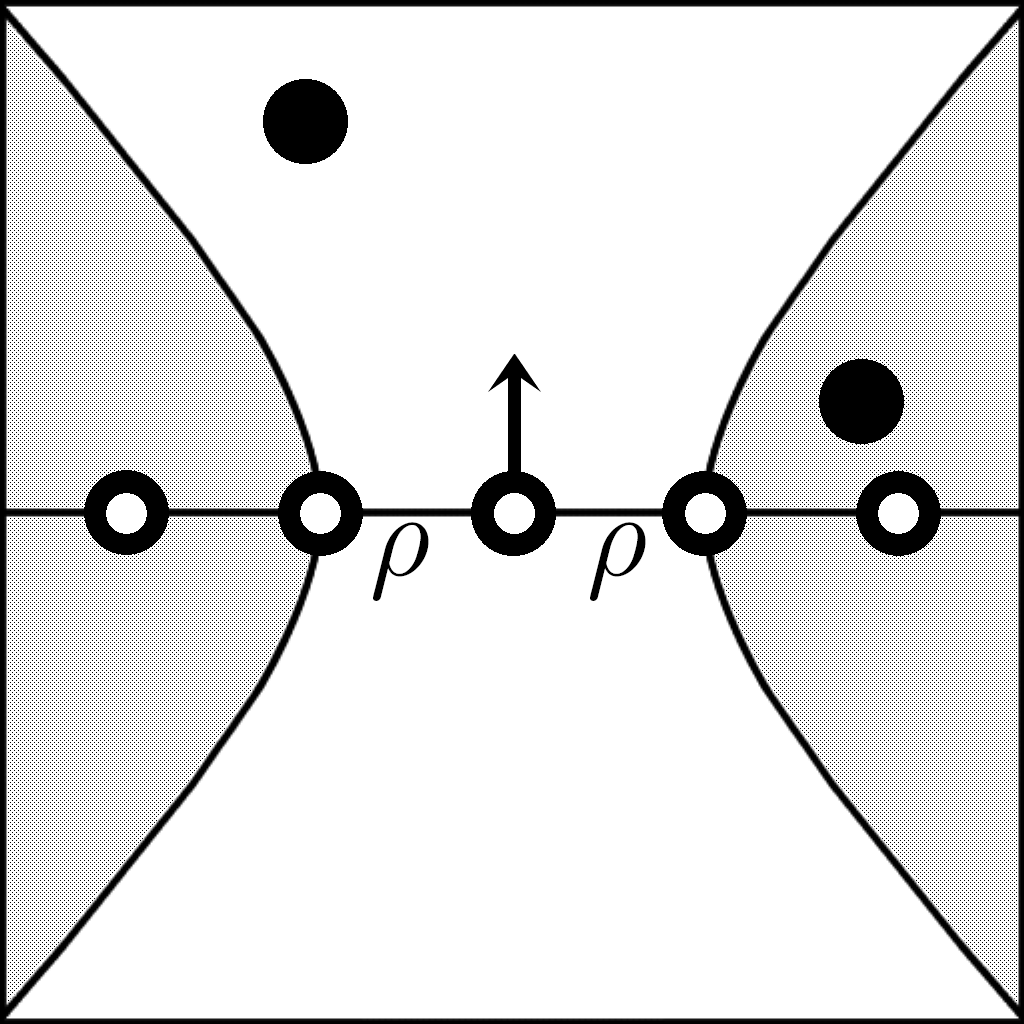
point-to-tangent plane rather than point-to-point. To eliminate incorrect vertex
pairings, a hyperboloid of one sheet was used as an exclusion surface. Fixed
surface points outside of the hyperboloid are discarded (Figure
5). The hyperboloid takes the original movable surface point
as the focus with normal vector as axis. The hyperboloid has a minimum radius of
to be known. A hard distance
threshold was set for all iterations, with surface distance measured
point-to-tangent plane rather than point-to-point. To eliminate incorrect vertex
pairings, a hyperboloid of one sheet was used as an exclusion surface. Fixed
surface points outside of the hyperboloid are discarded (Figure
5). The hyperboloid takes the original movable surface point
as the focus with normal vector as axis. The hyperboloid has a minimum radius of
![]() (voxel side length) and its asymptotic cone has a slope of
(voxel side length) and its asymptotic cone has a slope of ![]() with respect to the normal vector. The hyperboloid prevents point pairs with
nearly coincident surface tangent planes (indicating that the surfaces are
actually very close) from being discarded even when the the search distance
tolerance is slightly smaller than the voxel grid spacing (Figure
6).
with respect to the normal vector. The hyperboloid prevents point pairs with
nearly coincident surface tangent planes (indicating that the surfaces are
actually very close) from being discarded even when the the search distance
tolerance is slightly smaller than the voxel grid spacing (Figure
6).
|
In cases where the initial alignment is poor, it is often possible for the
registration process to reach positions which appear close to convergence, but
are not actually optimal. To deal with these situations, the implementation uses
the aforementioned 25 iterations of no improvement requirement (assuming valid
vertex pairs continue to be found). If the initial alignment is unusually bad
automatic registration may not be possible with this algorithm, due to local
minima in the optimization. In addition to tracking RMS distance, the number of
valid vertex pairs located each iteration is found. The final alignment is
chosen from the iteration with the best RMS where the vertex pair count is no
more than ![]() less than the maximum found during any iteration. This prevents
a bad alignment from appearing excellent with a very small RMS due to only a
tiny set of vertex pairs actually being used in the calculation.
less than the maximum found during any iteration. This prevents
a bad alignment from appearing excellent with a very small RMS due to only a
tiny set of vertex pairs actually being used in the calculation.
The application used to run the experiment was coded in C++ and compiled
with Microsoft Visual C++ Enterprise Edition. The experiment was run on a
custom built PC with AMD Athlon 1900+ XP processor, 1GB DDR 2100 RAM and running
Microsoft Windows 2000 Professional Edition. The surfaces used were generated
from stone dental replicas using the Steinbichler COMET 100 optical digitizer,
with ![]() lateral resolution and
lateral resolution and ![]() depth resolution.
depth resolution.
| Config. | |
KD | Octree | Barnes-Hut | Approx. KD |
| 1 | 65 | 0.031 | 0.078 | 0.329 | 0.391 |
| 130 | 0.812 | 2.219 | 0.343 | 0.375 | |
| 260 | 0.875 | 2.453 | 0.344 | 0.391 | |
| 520 | 1.047 | 3.000 | 0.344 | 0.375 | |
| 1040 | 1.266 | 3.829 | 0.344 | 0.390 | |
| 2 | 65 | 1.156 | 3.656 | 0.937 | 1.063 |
| 130 | 1.641 | 4.844 | 0.703 | 0.765 | |
| 260 | 1.875 | 4.875 | 0.688 | 0.750 | |
| 520 | 3.063 | 6.750 | 0.657 | 0.750 | |
| 1040 | 2.625 | 8.625 | 0.750 | 0.766 | |
| 3 | 65 | 0.609 | 2.000 | 0.281 | 0.281 |
| 130 | 2.547 | 7.281 | 1.000 | 1.109 | |
| 260 | 2.109 | 5.829 | 0.797 | 0.922 | |
| 520 | 2.250 | 7.140 | 0.781 | 0.953 | |
| 1040 | 2.938 | 9.110 | 0.750 | 0.969 | |
| 4 | 65 | 0.750 | 2.546 | 0.328 | 0.328 |
| 130 | 1.109 | 3.579 | 0.516 | 0.531 | |
| 260 | 1.844 | 4.781 | 0.672 | 0.765 | |
| 520 | 1.875 | 5.328 | 0.562 | 0.657 | |
| 1040 | 2.125 | 6.734 | 0.578 | 0.672 | |
| 5 | 65 | 0.531 | 1.719 | 0.266 | 0.265 |
| 130 | 0.531 | 2.750 | 0.422 | 0.313 | |
| 260 | 0.735 | 3.406 | 0.453 | 0.562 | |
| 520 | 2.906 | 7.234 | 0.813 | 1.031 | |
| 1040 | 2.828 | 7.875 | 0.687 | 0.844 | |
| 6 | 65 | 0.547 | 1.797 | 0.266 | 0.360 |
| 130 | 0.656 | 1.969 | 0.265 | 0.281 | |
| 260 | 1.375 | 3.922 | 0.625 | 0.437 | |
| 520 | 1.094 | 8.437 | 0.985 | 0.391 | |
| 1040 | 3.390 | 9.157 | 0.812 | 0.969 | |
| Median | 1.321 | 4.352 | 0.602 | 0.610 | |
| Mean | 1.571 | 4.764 | 0.577 | 0.622 | |
| SD | 0.928 | 2.554 | 0.232 | 0.274 | |
In nearly all configurations tested, the Barnes-Hut trees and approximation
KD-trees performed surface pair registration faster than traditional methods,
Table 3. The only exception was for perfect initial registration
(Configuration 1) at ![]() , where every other method converged on the first
iteration while the approximation methods took the 25 iteration algorithm
minimum for non-zero RMS distance calculations. There are a few other small
search distance configurations where methods are close in performance, however,
in general the approximation methods are at least twice as fast as the other
methods.
, where every other method converged on the first
iteration while the approximation methods took the 25 iteration algorithm
minimum for non-zero RMS distance calculations. There are a few other small
search distance configurations where methods are close in performance, however,
in general the approximation methods are at least twice as fast as the other
methods.
| Method | Median | Mean | |
| KD-Tree | 0.065 | 2.617 | |
| Octree | 0.063 | 2.286 | |
| Barnes-Hut Tree | 0.043 | 2.146 | |
| Approx. KD-Tree | 0.031 | 2.418 |
A somewhat surprising result shown in Table 4 is that Barnes-Hut approximation yielded the most precise registrations, though by only slight margin. This is likely due to the inherent biases in using only voxel coordinates for searching, with the local averaging done by the Barnes-Hut tree possibly overcoming these biases. Also surprising is that all three KD-tree based methods gave the worst mean registrations, though again by only small amounts. This may not be representative because approximation KD-trees conversely had the smallest median RMS distance.
Some explanation is in order for the large differences between the mean and median RMS distances in each configuration. The results for each individual test are not shown because there are very few differences in registration quality between the different search methods; the aggregate statistics provide the best comparison. For each test the surfaces generally align either quite well or not well at all. The alignment process tends to fail completely with surfaces that start out far apart or use a too small search distance tolerance. For each search method more than half of the tests achieved good registration leading to a small median RMS. The mean RMS along with the standard deviation are strongly influenced by the minority of failed registrations which have RMS distances orders of magnitude greater than successful registrations, leading to the large disparity.
Barnes-Hut trees have been shown to be an extremely effective structure for fast registration of pointclouds that may be misaligned by small to moderate amounts. The only significant drawback is the memory requirements compared to traditional search trees. For this reason approximation KD-trees are not recommended for use in pointcloud registration in three dimensions, as they offer no discernible advantages over Barnes-Hut tree and require slightly more memory. Approximation KD-trees likely offer a suitable general purpose solution for registration in higher dimensional space, as shown in [9] for general purpose nearest-neighbor search. Traditional KD-trees offer a fair compromise between memory usage and performance. Octrees are not recommended, as the only advantage over KD-trees are halved memory usage (less if total memory used, including pointcloud data, is considered).
This study was supported in part by USPHS Research Grant R01 DE-12225-05 from the National Institute of Dental and Craniofacial Research, National Institutes of Health, Bethesda, MD 20892, and the Minnesota Dental Research Center for Biomaterials and Biomechanics.